§2.3 幂函数
一、教学目标
1、知识与技能目标：
理解幂函数的概念，通过具体实例了解幂函数的图像和性质，并能进行初步的应用。
2、过程与方法目标：
通过幂函数的图象探究它们的性质，培养学生抽象概括的能力。
3、情感、态度与价值观目标：
通过观察幂函数的图像，体会教学的对称美；并通过计算机在辅助学习中的应用，激发学生的学习热情。
二、教学重点与难点
教学重点：从五个具体的幂函数中认识幂函数的基本性质．
教学难点：画五个幂函数的图象并由图象概括其性质．
三、教学用具
多媒体辅助教学
四、教学过程
一、问题引入
在下列几个问题中，建立
与
的函数关系式（用含有的式子表示）：
1.张红购买了每千克
元的蔬菜千克，她需要的钱为元； 
2.一个正方形的边长为，它的面积为；
3.一个正方体的边长为，它的体积为
4.一个正方形场地的面积为，这个正方形的边长为； 
5.一个人在
内骑车行进了
，那么他的平均速度为
. 
讨论：以上五个问题中的函数具有什么共同特征？
它们具有的共同特征：幂的底数是自变量，指数是常数．
从上述函数中，我们观察到，它们都是形如
的函数．
上述五个函数的共同特征中归纳出一个函数的通式
二、师生合作，共同探究：
1．幂函数的概念
一般地，函数
叫做幂函数，其中
是自变量，
是常数．
对于幂函数，我们只讨论
时的情形．
2．幂函数的图象
先让学生分别作出幂函数
，，，
，的图象．
展示函数的图象的作图动画过程．
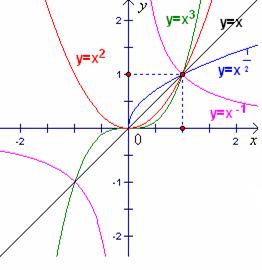
再展示在同一直角坐标系内幂函数，，，，的图象．
让学生观察图象，完成幂函数性质的表格．
|
|
|
|
|
|
|
|
定义域 |
|
|
|
|
|
|
值 域 |
|
|
|
|
|
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
非奇非偶函数 |
奇函数 |
|
单调性 |
增函数 |
|
增函数 |
增函数 |
|
|
公共点 |
|
||||
减
减
巩固练习
1.下列所给的函数中，不是幂函数的是
A．
B．
C．
D．
2.函数
是幂函数，则
的值为
.
3.无论
取何值，函数
的图象必经过的点是
.
4.已知下列几个函数 ①②③④⑤⑥
其中是奇函数的有 偶函数的有 (写出所有符合条件的序号) .
5.比较下列各组数中两个值的大小.
⑴
与
⑵
与
⑶
与
解析： 1. D （D选项是指数函数）
2.
或
（根据幂函数的定义，得
，得
或
3.
4.奇函数的有①②④⑥；偶函数的有③⑤
5. ⑴
； ⑵
⑶
（利用幂函数的单调性来比较值得大小）
提升练习
证明幂函数
在
上是增函数.
分析：用证明函数单调性的一般方法与步骤来完成证明.
证明：任取
，
，且
，则
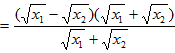
因为
，
，
所以
，即幂函数在上是增函数.
课时小结
1．幂函数的概念：函数
叫做幂函数，其中是自变量，是常数．
（这里只研究的情形）
2．幂函数，，，，的图象及其性质．
板书设计
1．幂函数的概念
函数叫做幂函数，其中是自变量，是常数．
2．幂函数，，，，的图象及其性质．