一、选择题(本大题共10小题,每小题4分,共40.0分,在每小题四个选项中只有一项是符合题目要求的)
1.
已知等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]()
![]()
A. 12 B. 16 C. 20 D. 24
【答案】C
【解析】解:设等差数列![]() 的公差为d,
的公差为d,![]() ,
,![]() ,
,![]() ,解得
,解得![]() .
.
则![]() ,
,
故选:C.
利用等差数列的通项公式及其性质即可得出.
本题考查了等差数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.
2.
如图是某几何体的三视图,则这个几何体是![]()
![]()

A. 三棱柱
B.
圆柱
C.
正方体
D.
三棱锥
|
|
【答案】A
【解析】解:由已知中的三视图中有两个矩形,
可得该几何体为柱体,
再由俯视图为三角形,
可得该几何体为三棱柱,
故选:A
根据三视图中有两个矩形,可得该几何体为柱体,再由俯视图为三角形,可得该几何体为三棱柱.
本题考查的知识点是简单几何体的三视图,难度不大,属于基础题.
3.
已知函数![]() ,则零点所在的区间可以为
,则零点所在的区间可以为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】【分析】
本题考查函数零点区间的判断,判断的主要方法是利用零点存在性定理,判断函数在给定区间端点处的符号是否相反.
【解答】
解:![]() 在R上单调递增,
在R上单调递增,
又![]() ,
,![]() ,
,![]() ,由函数的零点存在性定理可知,函数的零点所在的一个区间是
,由函数的零点存在性定理可知,函数的零点所在的一个区间是![]()
故选B.
4.
设集合![]() 2,3,4,
2,3,4,![]() 为全集,
为全集,![]() 2,
2,![]() ,
,![]() ,则
,则![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】解:![]() 集合
集合![]() 2,3,4,
2,3,4,![]() ,
,![]() ,
,
![]() 3,
3,![]() ,
,
又![]() 2,
2,![]() ,
,![]() ,
,
故选D.
由题意和补集、交集的运算分别求出![]() B、
B、![]() .
.
本题考查了交、并、补集的混合运算,属于基础题.
5.
过点![]() 且与直线
且与直线![]() 平行的直线方程为
平行的直线方程为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】【分析】
本题主要考查了两直线平行,两直线的k相等这一知识点![]() 根据平行直线的k相等,可设所求直线是
根据平行直线的k相等,可设所求直线是![]() 是常数,且
是常数,且![]() ,然后将已知条件代入求出b值,再把b值代入求该直线的解析式.
,然后将已知条件代入求出b值,再把b值代入求该直线的解析式.
【解答】
解:![]() 所求直线与直线
所求直线与直线![]() 平行,
平行,![]() 所求直线的k与直线
所求直线的k与直线![]() 相等,
相等,![]() 可设所求直线是
可设所求直线是![]() 是常数,且
是常数,且![]() ,又
,又![]() 该直线经过点
该直线经过点![]() ,
,![]() ,解得
,解得![]() ;所以该直线是:
;所以该直线是:![]() ,
,
故选A.
6.
在不等式![]() 表示的平面区域内的点是
表示的平面区域内的点是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】解:![]() 不等式
不等式![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
故选:B.
根据二元一次不等式表示平面区域,即可进行得到结论.
本题主要考查二元一次不等式表示平面区域以及点与平面区域的关系的判断,比较基础.
7. 从某校高三100名学生中采用系统抽样的方法抽取10名学生作代表,学生的编号从00到99,若第一组中抽到的号码是03,则第三组中抽到的号码是( )
A. 22 B. 23 C. 32 D. 33
【答案】B
【解析】解:根据系统抽样方法的特点,
从100名学生中抽取10名学生,组距是![]() ,
,
当第一组中抽到的号码是03时,第三组中抽到的号码是
![]() .
.
故选B.
根据系统抽样方法的特点,先求出组距是多少,再求第三组中抽到的号码是什么.
本题考查了系统抽样的应用问题,系统抽样的间隔相等,所以抽出的样本在总体中的分布是均匀的.
8.
已知向量![]() ,
,![]() ,若
,若![]() ,则
,则![]()
![]()
A. 2 B. ![]() C. 1 D.
C. 1 D. ![]()
【答案】B
【解析】解:![]() ;
;
![]() ;
;
![]() .
.
故选:B.
根据![]() 即可得出
即可得出![]() ,进行数量积的坐标运算即可求出x的值.
,进行数量积的坐标运算即可求出x的值.
考查向量垂直的充要条件,以及向量数量积的坐标运算.
9.
要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象
的图象![]()
![]()
A. 横坐标缩小为原来的![]() 倍,再向左平移
倍,再向左平移![]() 个单位
个单位
B.
横坐标扩大为原来的2倍,再向左平移![]() 个单位
个单位
C.
横坐标缩小为原来的![]() 倍,再向左平移
倍,再向左平移![]() 个单位
个单位
D.
横坐标扩大为原来的2倍,再向左平移![]() 个单位
个单位
【答案】C
【解析】解:要得到函数![]() 的图象,
的图象,
只需将函数![]() 的图象的横坐标缩小为原来的
的图象的横坐标缩小为原来的![]() ,
,
得到:![]() ,
,
再把函数的图象再向左平移![]() 个单位,
个单位,
得到:![]() ,
,
故选:C.
直接利用三角函数关系式的平移和伸缩变换求出结果.
本题考查的知识要点:三角函数关系式的恒等变变换,平移和伸缩变换的应用,主要考查学生的运算能力和转化能力,属于基础题型.
10.
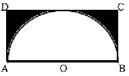
如图,长方形ABCD中,![]() ,
,![]() ,半圆的直径为
,半圆的直径为![]() 在长方形ABCD内随机取一点,则该点取自阴影部分的概率是( )
在长方形ABCD内随机取一点,则该点取自阴影部分的概率是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
【答案】B
【解析】【分析】
本题考查了几何概型公式的运用,关键是明确几何测度,利用面积比求之.
由几何概型,只要求出阴影部分的面积,利用面积比求概率.
【解答】
解:由题意,长方形的面积为![]() ,半圆面积为
,半圆面积为![]() ,
,
所以阴影部分的面积为![]() ,
,
由几何概型公式可得该点取自阴影部分的概率是![]() .
.
故选B.
二、填空题(本大题共5小题,每小题4分,共20.0分)
11. 比较大小![]() ______
______![]() .
.
【答案】![]()
【解析】解:因为![]() 为增函数,且
为增函数,且![]() ,
,
所以小![]() ,
,
故答案为:![]()
根据函数单调性即可比较.
本题考查了指数函数的单调性,属于基础题
12. 圆![]() 的圆心坐标是______.
的圆心坐标是______.
【答案】![]()
【解析】解:根据题意,圆![]() 的圆心为
的圆心为![]() ;
;
故答案为:![]()
根据题意,由圆的标准方程的形式分析可得答案.
本题考查圆的标准方程,注意圆标准方程的形式即可,属于基础题.
13. 如图所示的流程图中,若输入x的值为![]() ,则输出c的值为 .
,则输出c的值为 .

|
|
【答案】4
【解析】【分析】
本题考查程序框图,利用循环顺序,求得满足t条件的x的值,即可得到c的值.
【解答】
解:输入![]() ,不满足条件,循环得
,不满足条件,循环得![]() ,
,
不满足条件,循环得![]() ,
,
不满足条件,循环得![]() ,
,
此时满足条件![]() ,
,![]() ,输出
,输出![]() ,
,
故答案为4.
14. 已知角![]() 的终边经过点
的终边经过点![]() ,则
,则![]() 的值为
.
的值为
.
【答案】![]()
【解析】【分析】
本题考查三角函数的定义和诱导公式的应用,属于基础题.
先用诱导公式化简,再由三角函数的定义代入求值.
【解答】
解:![]() .
.
故答案为![]() .
.
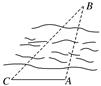
15. 如图,设A、B两点在河的两岸,一测量者在A的同侧,选定一点C,测出AC的距离为50 m,![]() ,
,![]() ,则A、B两点的距离为_______m。
,则A、B两点的距离为_______m。
【答案】![]()
【解析】【分析】
本题考查解三角形的实际应用,解题的关键是利用正弦定理,求三角形的边,属于中档题.
先利用三角形的内角和求出![]() ,再利用正弦定理,即可得出结论.
,再利用正弦定理,即可得出结论.
【解答】
解:在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
由正弦定理可得![]() ,
,
所以 ,
,
故答案为![]() .
.
三、解答题(本大题共5小题,共60.0分)
16. ![]() 本小题6分
本小题6分![]()
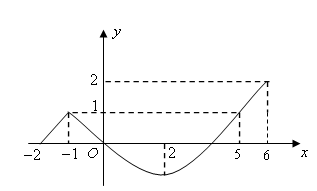
已知函数![]() 的图象如图、根据图象写出:
的图象如图、根据图象写出:
![]() 函数
函数![]() 单调递减区间;
单调递减区间;
![]() 满足不等式
满足不等式![]() 的解集.
的解集.
【答案】解:![]() 由图象知
由图象知![]() 的单调减区间为
的单调减区间为![]()
![]() 由图象知
由图象知![]() 的解集为
的解集为![]() 或
或![]() .
.
【解析】本题考查函数图象的应用及函数的单调区间.
![]() 由图象即可求解
由图象即可求解![]()
![]() 由图象即可求解.
由图象即可求解.
17. ![]() 本小题8分
本小题8分![]()
对某基本控制中心配发的出血热预防制剂进行检测,每盒共5支,其中一盒5支制剂的质量![]() 单位:
单位:![]() 茎叶图如下所示.
茎叶图如下所示.
![]() Ⅰ
Ⅰ![]() 求这盒制剂质量的平均数和中位数;
求这盒制剂质量的平均数和中位数;
![]() Ⅱ
Ⅱ![]() 如果从这盒制剂中随机取出2支使用,求取到的2支中至少有1支的质量为
如果从这盒制剂中随机取出2支使用,求取到的2支中至少有1支的质量为![]() 的既率.
的既率.

【答案】解:![]() Ⅰ
Ⅰ![]() 根据茎叶图知,数据的平均数为
根据茎叶图知,数据的平均数为
![]() ,
,
中位数为199;
![]() Ⅱ
Ⅱ![]() 如果从这盒制剂中随机取出2支,基本事件为
如果从这盒制剂中随机取出2支,基本事件为
![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,
![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,
共10种不同取法;
取到的2支中至少有1支的质量为![]() 的基本事件为
的基本事件为
![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,
![]() 、
、![]() ,
,![]() 、
、![]() ,共7种不同取法,
,共7种不同取法,
故所求的既率为![]() .
.
【解析】![]() Ⅰ
Ⅰ![]() 根据茎叶图计算数据的平均数和中位数;
根据茎叶图计算数据的平均数和中位数;
![]() Ⅱ
Ⅱ![]() 利用列举法求出基本事件数,计算所求的既率值.
利用列举法求出基本事件数,计算所求的既率值.
本题考查了茎叶图与平均数、中位数以及列举法求古典概型的概率问题,是基础题.
18. ![]() 本小题8分
本小题8分![]()
如图,在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() ,D,E分别是AB,PB的中点.
,D,E分别是AB,PB的中点.
![]() 求证:
求证:![]() 平面
平面![]()
![]() 求证:
求证:![]()
![]() 若
若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】证明:![]() ,E分别是AB,PB的中点
,E分别是AB,PB的中点
![]()
又![]() 平面PAC,
平面PAC,![]() 平面PAC
平面PAC
![]() 平面PAC;
平面PAC;
![]() 底面ABC,
底面ABC,![]() 底面ABC,
底面ABC,
![]()
又![]() ,
,![]() ,PC,
,PC,![]() 平面PBC
平面PBC
![]() 平面PBC
平面PBC
又![]() 平面PBC
平面PBC
![]() ;
;
解:![]() 由
由![]() 知,
知,![]() ,
,![]() ,
,
![]() 即为二面角
即为二面角![]() 的平面角
的平面角
![]() ,
,![]()
![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]()
【解析】本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的性质,解答![]() 的关键是熟练掌握空间线面关系的判定定理及性质,解答
的关键是熟练掌握空间线面关系的判定定理及性质,解答![]() 的关键是求出二面角的平面角.
的关键是求出二面角的平面角.
![]() 由D,E分别是AB,PB的中点,结合三角形中位线定理和线面平行的判定定理可得
由D,E分别是AB,PB的中点,结合三角形中位线定理和线面平行的判定定理可得![]() 平面PAC;
平面PAC;
![]() 由线面垂直的性质,可得
由线面垂直的性质,可得![]() ,结合
,结合![]() 和线面垂直的判定定理可得
和线面垂直的判定定理可得![]() 平面PBC,再由线面垂直的性质可得
平面PBC,再由线面垂直的性质可得![]() ;
;
![]() 由
由![]() 知,
知,![]() ,
,![]() ,故
,故![]() 即为二面角
即为二面角![]() 的平面角,解
的平面角,解![]() 可得答案.
可得答案.
19. ![]() 本小题8分
本小题8分![]()
已知![]() .
.
![]() 若
若![]() ,求角
,求角![]() 的值;
的值;
![]() 求
求![]() 的最小值.
的最小值.
【答案】解:![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,
即![]() ,
,
又![]() ,
,![]() ;
;
![]() ,
,
![]()
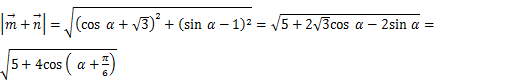 ,
,
![]() ,
,![]() ,
,
故当![]() 时,
时,![]() 取到最小值1.
取到最小值1.
【解析】本题主要考查了向量的数量积的应用,考查了向量的垂直以及向量的模,同时考查了三角函数的最值,属于中档题.
![]() 根据向量垂直得
根据向量垂直得![]() ,求出
,求出![]() ,再根据
,再根据![]() 的范围即可求出
的范围即可求出![]() ;
;
![]() 根据向量的模的公式进行化简,再根据
根据向量的模的公式进行化简,再根据![]() 的范围求解.
的范围求解.
20. ![]() 本小题10分
本小题10分![]()
已知数列![]() ,其前n项和
,其前n项和![]() 满足
满足![]() ,
,![]() .
.
![]() 求数列
求数列![]() 的通项公式;
的通项公式;
![]() 已知
已知![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
![]() 已知
已知![]() ,对任意
,对任意![]() ,都有
,都有![]() 成立,试确定实数
成立,试确定实数![]() 的取值范围.
的取值范围.
【答案】解:![]() 数列
数列![]() ,其前n项和
,其前n项和![]() 满足
满足![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 数列
数列![]() 是首项为3,公比为3的等比数列,
是首项为3,公比为3的等比数列,
![]() .
.
![]() ,
,
![]() 数列
数列![]() 的前n项和:
的前n项和:
![]() ,
,![]()
![]() ,
,![]()
![]() ,得:
,得:![]()
![]() ,
,
![]() .
.
![]() ,
,
对任意![]() ,都有
,都有![]() 成立,
成立,
![]() ,
,
即有![]() 恒成立.
恒成立.
当n为奇数时,![]() ,
,
由![]() 递增,可得
递增,可得![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
即有![]() ;
;
当n为偶数时,![]() ,由
,由![]() 递增,可得
递增,可得![]() 时,取得最小值
时,取得最小值![]() ,
,
即有![]() ,解得
,解得![]() ;
;
故实数![]() 的取值范围是
的取值范围是![]()
【解析】![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,从而
,从而![]() ,进而数列
,进而数列![]() 是首项为3,公比为3的等比数列,由此能求出
是首项为3,公比为3的等比数列,由此能求出![]() .
.
![]() 由
由![]() ,利用错位相减法能求出数列
,利用错位相减法能求出数列![]() 的前n项和
的前n项和![]() .
.
![]() 由
由![]() ,得
,得![]() 恒成立
恒成立![]() 由此能求出实数
由此能求出实数![]() 的取值范围.
的取值范围.
本题考查数列的通项公式的求法,考查实数的取值范围的求法,考查等差数列和等比数列的通项公式的运用、数列的单调性问题的解法等基础知识,考查运算求解能力、推理论证能力,考查分类讨论与整合思想、函数与方程思想,是中档题.